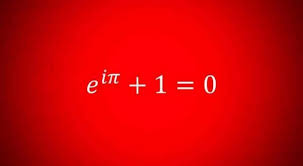Persamaan Euler (seperti tertera pada gambar di atas) kerap dikutip sebagai contoh keindahan matematis yang menawan. Tiga operasi aritmatika tertera di dalamnya, yakni penambahan, perkalian, dan eksponensial, plus tanda 'sama dengan'. Lebih dari itu. Di dalamnya ada pula angka ajaib 0 dan 1—bilangan berapapun bila dikalikan dengan 0 maka ia akan sirna, muksa, suwung, lenyap; dan bilangan berapapun bila dikalikan dengan 1 maka ia tetap jadi dirinya sendiri.
Juga ada π atau 3,14159265. Phi adalah simbol keajaiban lain yang merangkum di dalam dirinya keharmonisan struktur tubuh manusia yang menjadikannya makhluk indah. Lalu e yang jadi dasar dari logarithma natural, yang banyak digunakan dalam analisis matematis dan keilmuan lainnya. Ya, e = 2,718281828 juga memuat perulangan yang ritmis (18281828..). Begitulah, π dan e kerap disebut sebagai angka transendental. Euler juga memasukkan i, yang tak lain unit imajiner dari bilangan kompleks.
Leonhard Euler, matematikawan abad ke-18, begitu piawai dalam meringkus gagasan besar ke dalam persamaan yang terlihat sederhana. Apakah yang lebih mistis daripada angka imajiner yang berinteraksi dengan angka riil untuk menghasilkan nol—‘kosong, suwung, nihil, tiada’. Di sinilah letak keindahannya.
Di mata awam, persamaan Euler memang tidak menikmati ketenaran setara dengan persamaan Albert Einstein yang mashur itu: E = mc2. Bahkan, dibandingkan dengan persamaan Phytagoras sekalipun—yang kita mengakrabinya sejak lama ketika mulai memelajari geometri. Ya, a2 + b2 = c2. ‘Oldie but goodie’—kuno tapi tetap menawan. Persamaan ini meringkaskan teorema Phytagoras bahwa untuk setiap segitiga sama kaki, kuadrat dari hipotenus (sisi terpanjang) atau c sama dengan penjumlahan dari kuadrat panjang kedua sisi lainnya (a dan b).
Ada persamaan lain yang tak kalah menggoda, yakni 1 = 0,999999999... Sederhana? Ya. Tak banyak barangkali yang mencermati persamaan ini—persamaan yang, dalam kata-kata matematikawan Steven Strogatz, sederhana tapi provokatif. “Banyak orang tidak percaya bahwa itu benar,” ujarnya. Persamaan ini juga indah dalam kesetimbangannya. Sisi kiri mencerminkan permulaan matematika, dan sisi kanan mewakili misteri ketidakterbatasan.
Persamaan yang dirumuskan Maxwell meringkus pemahaman kita tentang gejala listrik dan magnet sebagai fenomena yang berjalin-berkelindan. Dalam kesederhanaannya, keempat persamaan Maxwell meringkus dan meringkaskan kompleksitas gagasan bahwa cahaya adalah gelombang elektromagnetik. Ia menyerap dan merangkumkan gagasan Gauss, Faraday, dan Ampere.
Demikianlah, sederhana itu indah, terutama bila kita menyadari kompleksitas di baliknya.
Namun bagaimana dengan persamaan ini: (x2 + y2 -1)3 –x2y3 = 0. Coba tuangkan ke atas secarik kertas grafik dan lihatlah gambar yang muncul. Menurut Anda, apakah persamaan ini juga indah? ***
Ikuti tulisan menarik dian basuki lainnya di sini.